換算質量µの求め方は、式を覚えておけば、難しくはない。式だけ知りたい人は下まで飛ばして。

意味自体は特殊相対性理論と深く関係してる。

それについても軽く書いてみるよ。

そもそも換算質量とは？

普通の質量は、物体が静止している場合の質量を指す。

一方、

換算質量は、物体が運動エネルギーを持っている場合や、相対論的な速度で運動している場合における質量を表す。

相対論的な速度は、ある物体が運動している状態から見たもう一つの物体の速度のことね。

ここで気になるのが次の疑問。

動いている物体の質量

質量って、動いても変わらないんじゃないの？

ここで、必要な概念として特殊相対性理論が出てくる。

具体的には、質量 m の物体が速度 v で運動している場合、その質量 m′ は以下のようになる。

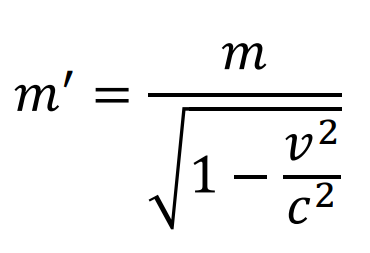
cは光速、定数だね。

つまり式から物体が速度を持つとその質量が増加することがわかるね。

換算質量µの求め方

質量 m_1​ と m₂ の二つの物体が互いに静止していて、それらが相対速度 v で衝突する場合、衝突後の合成物体の換算質量 µ は以下のように表される。

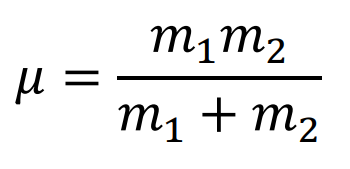
代入すれば求められるよに。