波動関数の規格化は量子力学の中でも重要な概念!
問題としても、波動関数を規格化する問題や、証明がよく問われる。
覚えとけば難しくないから書いてみるね。
波動関数の規格化とは?
波動関数Ψ(x)の規格化とは全空間[-∞,∞]において次の条件を満たす
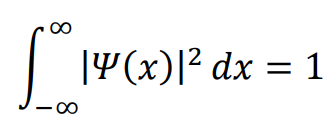
ここで|Ψ(x)|2は波動関数の絶対値の二乗を表し、確率密度を表してるよ。
意味的には、波動関数が表す粒子が位置xに存在する確率の総和が1であることを意味してる。
つまり、どこかしらに粒子が存在するってこと。
ただの波動関数は粒子が存在する確率を明確に言及できないから、規格化された波動関数は扱いやすいってイメージ。
規格化する方法
次のステップで規格化できる。
- 規格化されてない波動関数Ψ(x)をΨ(x)=NΦ(x)とおく。
- 規格化条件に代入
- Nを求めて、規格化完了!
すんごく簡単にできるよ。一問例示すね。
例
区間 [−1,1]上の規格化されてない波動関数Ψ(x)=2xの規格化。
1.Ψ(x)=N2x
2.規格化条件に代入
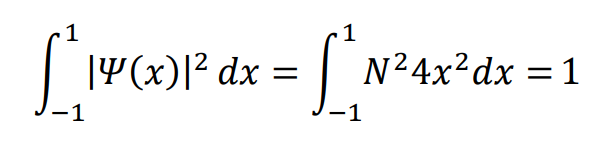
3.Nを求めて
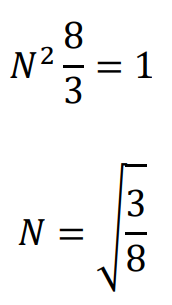
規格化完了!
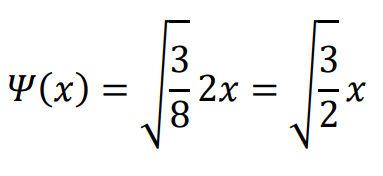
慣れれば簡単だよ。直交性とごっちゃにならないようにね。
直交性についてもまとめたから見てみてね。




コメント