量子力学において、よーく見る波動関数。
波動関数には、一価性、連続性、有限性の3つの条件が必要なんだ。
それぞれ解説してみるよ。
一価性とは
一価性とは、その関数が物理的に意味のある単一の値を持つこと。
簡単に言うと、与えられた値xには対応した1つの値Ψ(x)が定まるってこと。
これの何がいいのか?
例えば、ある範囲内の波動関数が一価性を持ってたとする。
各座標に対応する値、つまり、その範囲内に波動関数で表された粒子が存在してるってことがわかるんだ。
量子力学は確率的な話であるため、粒子が確かに存在することは、重要な意味をもつ。
範囲内に粒子があるかわからんと、計算も予測も信憑性ないしね。
連続性とは
連続性とは、波動関数が滑らかで断続がない。つまり、波動関数の値や微分が連続的に変化すること。
これは量子力学の基本的な方程式であるシュレディンガー方程式を見れば理由がわかる。
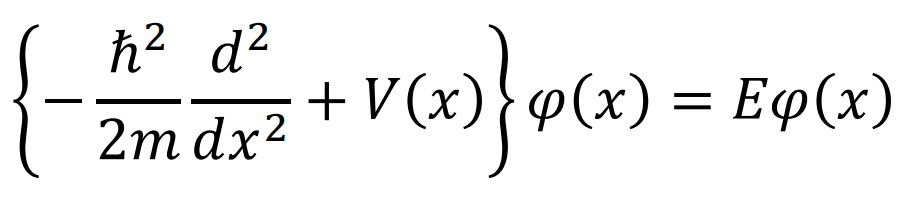
二階微分が含まれていることがわかるね。
微分の定義として、微分が可能な時は、連続性を持つ。
したがって、波動関数の連続性が必要なんだ。
有限性
有限性とは、波動関数の物理的な意味での確率密度が有限であること。
量子力学では、波動関数が特定の範囲で定義され、その範囲内での粒子の振る舞いや性質を記述する。
したがって、確率密度が有限になるのも納得できる。
確率が無限だったら考えようないしね。



コメント