すごく限定的なんだけど、課題とかの助けになればって感じ。

やることはそんな難しくないから、順を追って説明してみる。

導出方法

∂/∂xを次のように変形

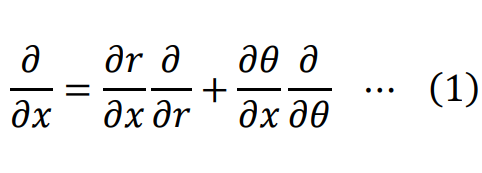
次にr²=x²＋y²をxで微分。

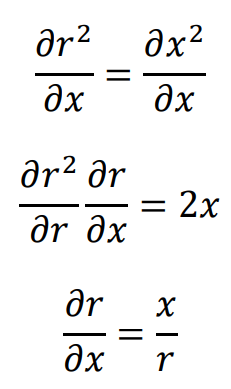
ここで、x=rcosθより

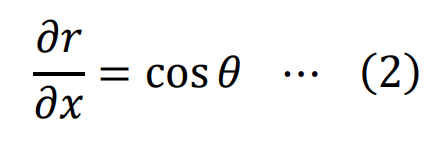
次に、tanθ=sinθ/cosθ=y/xの両辺にxcosθをかけると

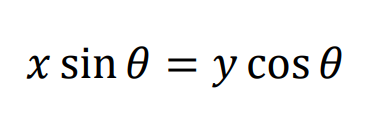
両辺をxで微分すると

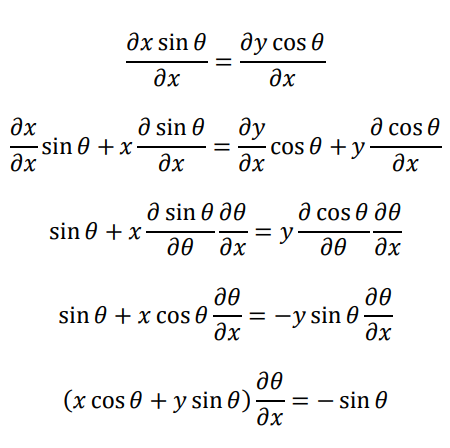
ここで、x=rcosθ,y=rsinθより

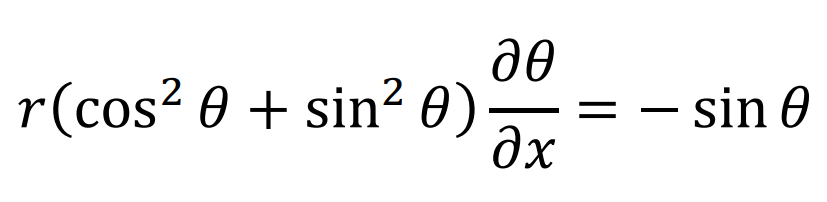
cos²θ+sin²θ=1より

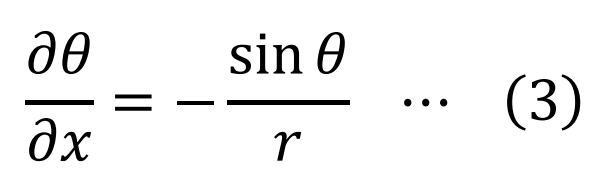
(1)に(2)と(3)を代入すると

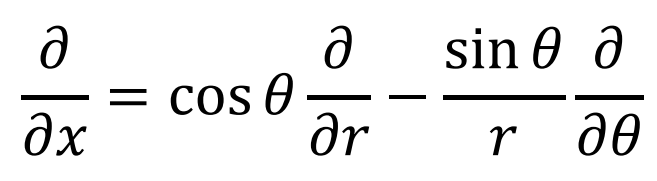
これで導出完了！意外と長くなっちゃった笑

∂/∂yも同じ手順で導出できるからやってみてね。

もっと課題手助けできるようなサイトめざします。