エネルギー固有値と固有関数は物理化学において重要。
内容としては基礎的だからなるべくわかりやすく説明するね。
それぞれの定義
ある演算子Aを関数f(x)に作用させた結果が、元の関数f(x)と定数倍の関係にあるとき、その関数を
固有関数と呼び、定数を固有値と呼ぶ。
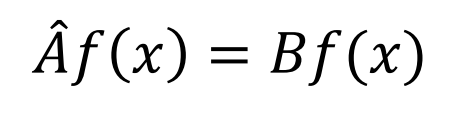
つまり、この式ではf(x)が固有関数、Bが固有値ってこと。
イメージとしては、演算子Aを作用させたとき、それぞれの関数に、それぞれ対応した値が得られる。カップルみたいな感じ。
ちなみに演算子Aの上についてる^はハットて呼ばれてて、演算子だと示す印みたいなもの。
演算子についてはこれみてみてね。
具体例
一番よく見る例としては、シュレディンガー方程式だと思う。
一次元におけるシュレディンガー方程式は次のように表される。
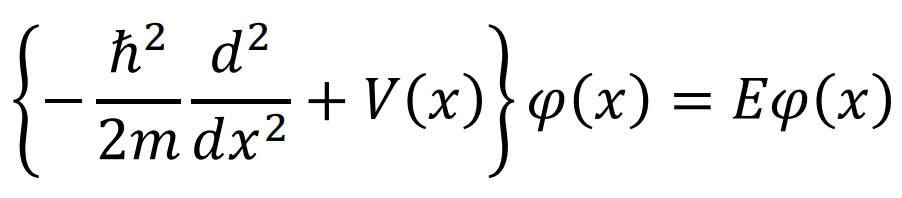
一見、関係ないように見えるけど、演算子が隠れてる。
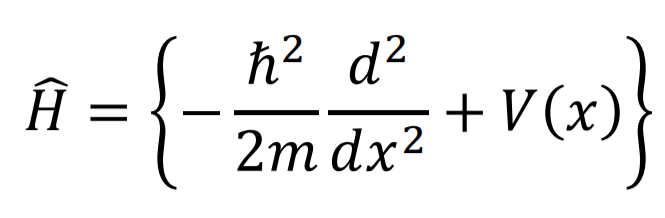
このHはハミルトニアンって呼ばれてる演算子。書き換えると
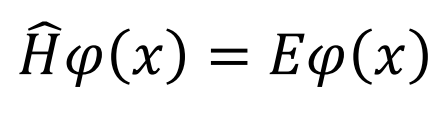
さっきと同じ形になったでしょ。φ(x)が固有関数、Eが固有値って感じ。
大学の授業って当たり前のように演算子出してくるから腹立つよね。




コメント